Zadanie nr 9456431
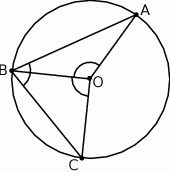
Na okręgu o środku w punkcie 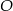 leżą punkty
leżą punkty 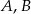 i
i 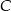 (zobacz rysunek). Kąt
(zobacz rysunek). Kąt 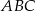 ma miarę
ma miarę 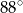 , a kąt
, a kąt 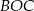 ma miarę o
ma miarę o 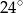 mniejszą od miary kąta
mniejszą od miary kąta 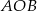 .
.
Kąt 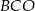 ma miarę
ma miarę
A) 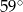 B)
B) 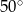 C)
C) 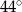 D)
D) 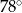
Rozwiązanie
Zauważmy najpierw, że każdy z trójkątów 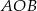 i
i 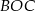 jest równoramienny. Oznaczmy
jest równoramienny. Oznaczmy 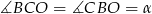 . Wtedy
. Wtedy
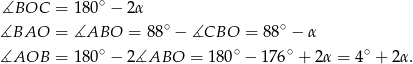
Stąd
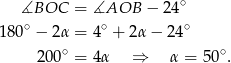
Odpowiedź: B

