Zadanie nr 9585513
Na okręgu o środku 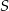 leżą punkty
leżą punkty 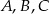 i
i 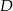 . Odcinek
. Odcinek 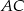 jest średnicą tego okręgu. Kąt między tą średnicą a cięciwą
jest średnicą tego okręgu. Kąt między tą średnicą a cięciwą 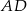 jest równy
jest równy 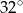 (zobacz rysunek).
(zobacz rysunek).
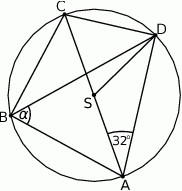
Kąt  między cięciwami
między cięciwami 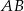 i
i 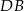 jest równy
jest równy
A) 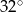 B)
B) 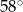 C)
C) 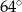 D)
D) 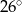
Rozwiązanie
Sposób I
Trójkąt 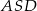 jest równoramienny (bo
jest równoramienny (bo 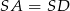 ), więc
), więc
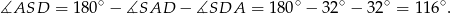
Interesujący nas kąt 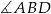 jest oparty na tym samym łuku, co kąt
jest oparty na tym samym łuku, co kąt 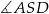 , więc
, więc
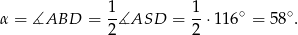
Sposób II
Zauważmy, że trójkąt 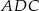 jest prostokątny (bo kąt
jest prostokątny (bo kąt 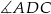 jest oparty na średnicy). Ponadto kąty
jest oparty na średnicy). Ponadto kąty 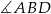 i
i 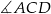 są oparte na tym samym łuku, więc
są oparte na tym samym łuku, więc
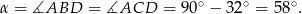
Odpowiedź: B

