Zadanie nr 9828928
Punkty 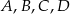 leżą na okręgu o środku
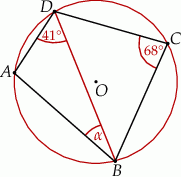
leżą na okręgu o środku 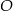 (zobacz rysunek). Miara zaznaczonego kąta
(zobacz rysunek). Miara zaznaczonego kąta  jest równa
jest równa
A) 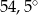 B)
B) 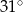 C)
C) 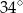 D)
D) 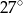
Rozwiązanie
Sposób I
Czworokąt 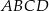 jest wpisany w okrąg, więc
jest wpisany w okrąg, więc
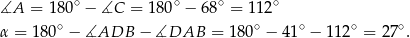
Sposób II
Dorysujmy przekątną 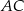 .
.
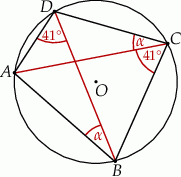
Ponieważ kąty wpisane oparty na tym samym łuku są równe, mamy
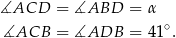
Zatem

Odpowiedź: D

