Zadanie nr 9829405
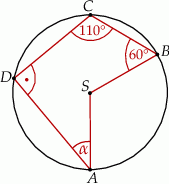
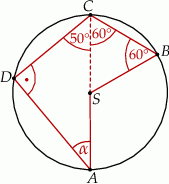
Punkty 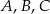 i
i 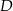 leżą na okręgu o środku
leżą na okręgu o środku 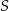 . Miary kątów
. Miary kątów 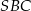 ,
, 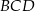 ,
, 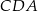 są równe odpowiednio:
są równe odpowiednio: 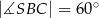 ,
, 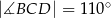 ,
, 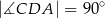 (zobacz rysunek).
(zobacz rysunek).
Wynika stąd, że miara  kąta
kąta 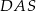 jest równa
jest równa
A) 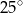 B)
B) 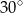 C)
C) 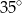 D)
D) 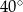
Rozwiązanie
Trójkąt 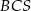 jest równoramienny (bo
jest równoramienny (bo 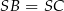 ) i jeden z jego kątów ma miarę
) i jeden z jego kątów ma miarę 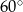 , więc jest to trójkąt równoboczny.
, więc jest to trójkąt równoboczny.
Zatem
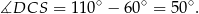
Sposób I
Wiemy, że trójkąt 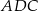 jest prostokątny, więc jego przeciwprostokątna
jest prostokątny, więc jego przeciwprostokątna 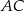 jest średnicą danego okręgu. W szczególności punkty
jest średnicą danego okręgu. W szczególności punkty 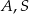 i
i 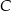 leżą na jednej prostej. Stąd
leżą na jednej prostej. Stąd
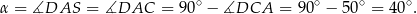
Sposób II
Dorysujmy jeszcze promień  .
.
Każdy z trójkątów 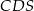 i
i 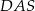 jest równoramienny, więc
jest równoramienny, więc
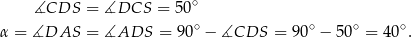
Odpowiedź: D

