/Szkoła średnia/Zadania testowe/Geometria/Planimetria/Trójkąt

Zadanie nr 3236898

Dodaj do ulubionych
Dodaj do rozwiązanych

W trójkącie prostokątnym naprzeciw kąta ostrego α leży przyprostokątna długości 3 cm. Natomiast przeciwprostokątna ma długość 6 cm. Zatem
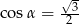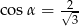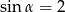A) √- cosα = -3- 2 B) cos α = √2- 3 C) sin α = 2 D) √ -- tg α = 3

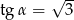
Rozwiązanie

Zaczynamy od rysunku

PIC

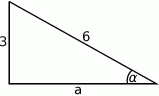
Sposób I

Z twierdzenia Pitagorasa obliczamy długość drugiej przyprostokątnej

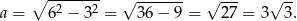
∘ ------- √ ------- √ --- √ -- a = 62 − 32 = 3 6− 9 = 27 = 3 3.

Liczymy wartości funkcji trygonometrycznych

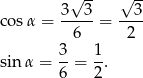
√ -- √ -- co sα = 3--3-= --3- 6 2 3 1 sin α = --= -. 6 2

Sposób II

Obliczamy wartość sinusa

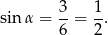
sin α = 3-= 1-. 6 2

Teraz z jedynki trygonometrycznej obliczamy wartość cosinusa

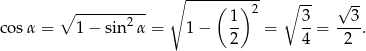
∘ ---------- ∘ ---------- ( )2 ∘ -- √ -- cos α = 1 − sin2 α = 1 − 1- = 3-= --3. 2 4 2

 
Odpowiedź: A

Wersja PDF