/Szkoła średnia/Zadania testowe/Zadania z treścią

Zadanie nr 9506325

Dodaj do ulubionych
Dodaj do rozwiązanych

Metalowa podstawka ma mieć kształt prostokąta o obwodzie 120 cm i polu największym z możliwych. Podstawka powinna mieć zatem wymiary
A) 25 cm na 35 cm B) 20 cm na 40 cm C) 60 cm na 60 cm D) 30 cm na 30 cm

Rozwiązanie

Sposób I

Obliczamy pola podstawek o podanych bokach

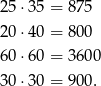
25 ⋅35 = 87 5 20 ⋅40 = 80 0 60 ⋅60 = 36 00 30 ⋅30 = 90 0.

Teraz można się nabrać, bo największe pole otrzymujemy dla podstawki 60 cm na 60 cm – taka podstawka ma jednak obwód 240 cm, a nie 120 cm!

Z podstawek o obwodzie 120 cm największe pole ma podstawka o bokach 30 cm na 30 cm.

Sposób II

Oznaczmy przez 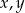x,y długości boków podstawki. Wówczas z warunku na obwód otrzymujemy

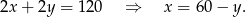
2x + 2y = 120 ⇒ x = 60 − y.

Chcemy, aby pole było jak największe, czyli szukamy największej wartości funkcji

P = x ⋅y.

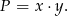
Podstawiamy z warunku na obwód i otrzymujemy

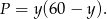
P = y(6 0− y).

Wykresem tej funkcji jest parabola o ramionach skierowanych w górę i pierwiastkach w punktach 0 i 60. Zatem największą wartość przyjmuje w wierzchołku, czyli dla

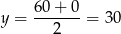
60 + 0 y = -------= 30 2

(dokładnie w środku między pierwiastkami). Stąd

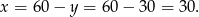
x = 60− y = 60 − 30 = 30.

Zatem największe pole ma prostokąt o bokach długości 30 cm na 30 cm.  
Odpowiedź: D

Wersja PDF