/Szkoła średnia/Zadania testowe/Równania/Układy równań

Zadanie nr 4392787

Liczby rzeczywiste 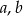a,b spełniają warunki: 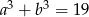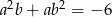3 3 a + b = 19 , 2 2 a b+ ab = − 6 . Wtedy suma 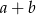a+ b jest równa
A) 37 B) 13 C) 1 D) 25

Wersja PDF

Rozwiązanie

Mamy tak naprawdę dany układ równań

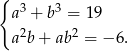
{ 3 3 a + b = 19 a2b+ ab2 = − 6.

Widać, że używając tych dwóch równań łatwo uzyskać prawą stronę wzoru

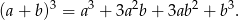
3 3 2 2 3 (a+ b ) = a + 3a b+ 3ab + b .

Mamy zatem

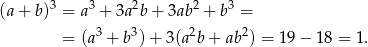
3 3 2 2 3 (a+ b) = a + 3a b+ 3ab + b = = (a3 + b3)+ 3(a2b+ ab2) = 19 − 18 = 1 .

Zatem 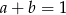a+ b = 1 .  
Odpowiedź: C

Wersja PDF