Zadanie nr 5274992
Układ równań 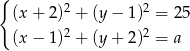 z niewiadomymi
z niewiadomymi 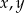 i parametrem dodatnim
i parametrem dodatnim  ma dwa rozwiązania, gdy
ma dwa rozwiązania, gdy
A) 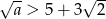 B)
B) 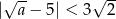 C)
C) 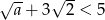 D)
D) 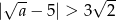
Rozwiązanie
Pierwsze równanie opisuje okrąg o środku 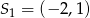 i promieniu
i promieniu 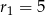 , a drugie okrąg o środku
, a drugie okrąg o środku 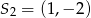 i promieniu
i promieniu 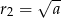 . Ponieważ
. Ponieważ
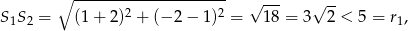
to środek drugiego okręgu znajduje się wewnątrz koła ograniczonego pierwszym okręgiem. Robimy szkicowy rysunek tej sytuacji
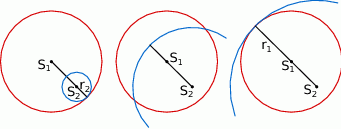
Sposób I
Z obrazka powinno być jasne, że drugi okrąg przecina pierwszy w dwóch punktach, gdy jego promień jest pomiędzy dwoma skrajnymi położeniami, w których drugi okrąg jest styczny do pierwszego, tzn. gdy
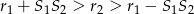
Warunek ten możemy zapisać w postaci
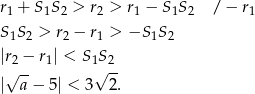
Sposób II
Sprawdzamy podane odpowiedzi.
Widać, że warunki 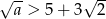 i
i 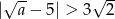 są spełnione przez dowolnie duże liczby
są spełnione przez dowolnie duże liczby  , a z obrazka jest jasne, że przy bardzo dużym promieniu drugiego okręgu jest on rozłączny z pierwszym okręgiem.
, a z obrazka jest jasne, że przy bardzo dużym promieniu drugiego okręgu jest on rozłączny z pierwszym okręgiem.
Podobnie, warunek 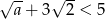 jest spełniony przez dowolnie małe liczby dodatnie
jest spełniony przez dowolnie małe liczby dodatnie  , a wtedy drugi okrąg będzie w całości zawarty w pierwszym okręgu. Pozostaje więc warunek
, a wtedy drugi okrąg będzie w całości zawarty w pierwszym okręgu. Pozostaje więc warunek 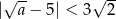 .
.
Odpowiedź: B

