Zadanie nr 5268090
Punkty 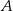 oraz
oraz 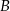 leżą na okręgu o środku
leżą na okręgu o środku 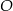 . Proste
. Proste 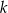 i
i 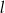 są styczne do tego okręgu w punktach – odpowiednio –
są styczne do tego okręgu w punktach – odpowiednio – 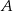 i
i 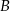 . Te proste przecinają się w punkcie
. Te proste przecinają się w punkcie 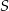 i tworzą kąt o mierze
i tworzą kąt o mierze 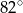 (zobacz rysunek).
(zobacz rysunek).
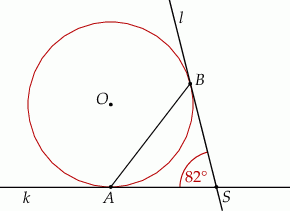
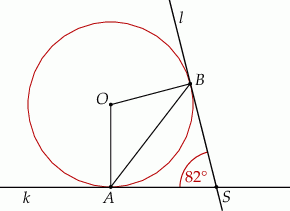
Miara kąta 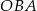 jest równa
jest równa
A) 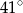 B)
B) 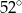 C)
C) 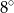 D)
D) 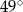
Rozwiązanie
Dorysujmy promienie 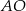 i
i 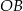 .
.
Sposób I
Suma kątów w czworokącie 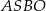 jest równa
jest równa 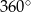 , więc
, więc
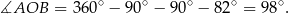
Patrzymy teraz na trójkąt równoramienny 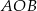 .
.
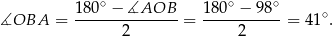
Sposób II
Trójkąt 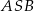 jest równoramienny, więc
jest równoramienny, więc
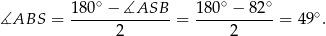
Kąt 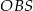 jest prosty, więc
jest prosty, więc
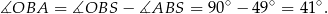
Odpowiedź: A

