Zadanie nr 2100863
Punkty 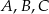 leżą na okręgu o środku
leżą na okręgu o środku 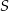 (rysunek),
(rysunek), 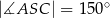 oraz
oraz 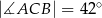 . Miara kąta
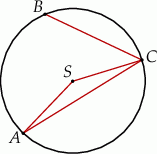
. Miara kąta 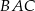 jest równa
jest równa
A) 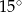 B)
B) 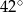 C)
C) 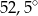 D)
D) 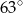
Rozwiązanie
Dorysujmy odcinek  .
.
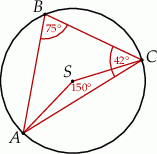
Korzystając z twierdzenia o kątach wpisanym i środkowym mamy
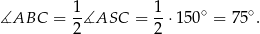
Suma kątów w trójkącie  jest równa
jest równa  , więc
, więc
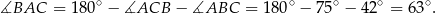
Odpowiedź: D

