Zadanie nr 4761185
Punkty 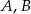 i
i 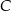 leżą na okręgu o środku
leżą na okręgu o środku 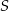 (zobacz rysunek).
(zobacz rysunek).
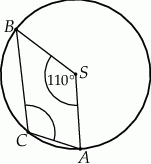
Miara zaznaczonego kąta wpisanego 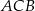 jest równa
jest równa
A) 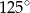 B)
B) 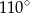 C)
C) 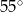 D)
D) 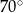
Rozwiązanie
Sposób I
Korzystamy z faktu, że kąt środkowy jest dwa razy większy od kąta wpisanego opartego na tym samym łuku (na danym obrazku jest to łuk 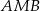 ).
).
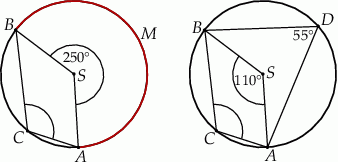
Zatem
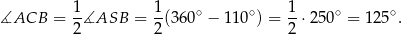
Sposób II
Jeżeli nie chcemy posługiwać się kątami wklęsłymi to dorysujmy punkt 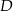 na na okręgu. Wtedy
na na okręgu. Wtedy
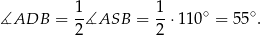
Zatem
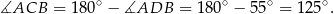
Odpowiedź: A

