Zadanie nr 7437638
Bok 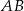 czworokąta
czworokąta 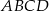 wpisanego w okrąg jest średnicą okręgu oraz
wpisanego w okrąg jest średnicą okręgu oraz 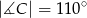 .
.
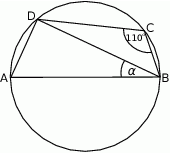
Zatem kąt  ma miarę
ma miarę
A) 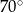 B)
B) 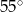 C)
C) 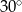 D)
D) 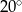
Rozwiązanie
Sposób I
Dorysujmy przekątną 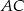 .
.
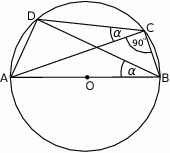
Kąt 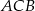 jest oparty na średnicy, więc ma miarę
jest oparty na średnicy, więc ma miarę 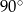 . Ponadto kąty
. Ponadto kąty 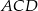 i
i 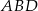 są oparte na tym samym łuku, więc mają równe miary. Mamy więc
są oparte na tym samym łuku, więc mają równe miary. Mamy więc
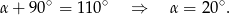
Sposób II
Kąt 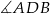 jest oparty na średnicy, więc
jest oparty na średnicy, więc 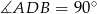 . Zatem
. Zatem
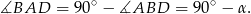
Teraz wystarczy skorzystać z tego, że w czworokącie wpisanym w okrąg sumy miar przeciwległych kątów są równe 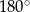 . Zatem
. Zatem
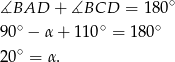
Odpowiedź: D

