/Szkoła średnia/Zadania testowe/Funkcje/Wielomiany

Zadanie nr 2609198

Dodaj do ulubionych
Dodaj do rozwiązanych

Dany jest wielomian 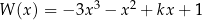3 2 W (x) = − 3x − x + kx + 1 , gdzie 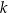k jest pewną liczbą rzeczywistą. Wiadomo, że wielomian 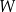W można zapisać w postaci 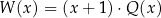W (x) = (x + 1) ⋅Q (x) dla pewnego wielomianu 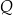Q . Liczba 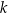k jest równa
A) 29 B) 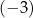(− 3) C) 0 D) 3

Rozwiązanie

Jeżeli 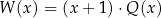W (x) = (x + 1) ⋅Q (x) , to

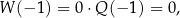
W (− 1) = 0 ⋅Q (−1 ) = 0,

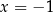czyli x = − 1 jest pierwiastkiem wielomianu 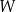W . Mamy zatem

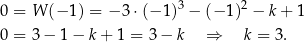
0 = W (−1 ) = − 3⋅(− 1)3 − (− 1)2 − k+ 1 0 = 3 − 1 − k + 1 = 3 − k ⇒ k = 3.

 
Odpowiedź: D

Wersja PDF