Zadanie nr 7703593
Pochodna funkcji 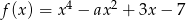 jest funkcją rosnącą jeżeli
jest funkcją rosnącą jeżeli
A) 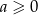 B)
B) 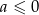 C)
C) 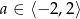 D)
D) 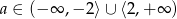
Rozwiązanie
Liczymy pochodną danej funkcji
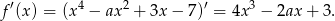
Jeżeli 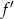 ma być rosnąca, to jej pochodna musi nieujemna. Liczymy tę pochodną
ma być rosnąca, to jej pochodna musi nieujemna. Liczymy tę pochodną
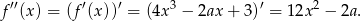
Wykresem otrzymanej funkcji jest parabola o ramionach skierowanych w górę i wierzchołku w punkcie 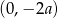 . Jeżeli funkcja
. Jeżeli funkcja 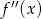 ma być nieujemna, to musimy mieć
ma być nieujemna, to musimy mieć 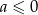 .
.
Odpowiedź: B

