/Szkoła średnia/Zadania testowe/Funkcje/Wielomiany

Zadanie nr 7897393

Dodaj do ulubionych
Dodaj do rozwiązanych

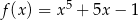
Funkcja określona dla każdej liczby rzeczywistej x wzorem 5 f(x) = x + 5x − 1
A) ma więcej niż dwa minima lokalne. B) ma dokładnie dwa minima lokalne.
C) ma dokładnie jedno minimum lokalne. D) nie ma minimum lokalnego.

Rozwiązanie

Liczymy pochodną funkcji 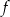f .

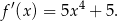
′ 4 f (x) = 5x + 5.

Ponieważ pochodna jest stale dodatnia, funkcja 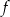f jest rosnąca w całej swojej dziedzinie. Nie ma więc ekstremów lokalnych.  
Odpowiedź: D

Wersja PDF