/Szkoła średnia/Zadania testowe/Funkcje/Wielomiany

Zadanie nr 9516125

Dodaj do ulubionych
Dodaj do rozwiązanych

Która z poniższych funkcji, określonych w zbiorze liczb rzeczywistych, nie ma minimum lokalnego ani maksimum lokalnego?
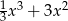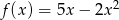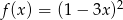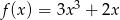
A) 13x 3 + 3x 2 B) f(x) = 5x− 2x2 C) f(x ) = (1− 3x)2 D) f (x) = 3x 3 + 2x

Rozwiązanie

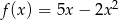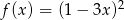Wykresami funkcji 2 f(x) = 5x− 2x i 2 f(x ) = (1− 3x) są parabole, więc każda z tych funkcji ma ekstremum lokalne. W przypadku pozostałych dwóch funkcji liczymy pochodne.

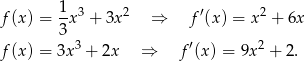
f(x ) = 1x 3 + 3x 2 ⇒ f′(x) = x 2 + 6x 3 f(x ) = 3x3 + 2x ⇒ f′(x) = 9x2 + 2.

Widać teraz, że druga z tych funkcji jest rosnąca (bo pochodna jest dodatnia), więc nie ma ona ekstremów lokalnych.  
Odpowiedź: D

Wersja PDF