/Szkoła średnia/Zadania testowe/Geometria/Planimetria/Trójkąt/Prostokątny/Oblicz długość

Zadanie nr 3296159

Dodaj do ulubionych
Dodaj do rozwiązanych

W trójkącie prostokątnym o przyprostokątnych długości 5 i 12 połączono wierzchołek 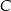C kąta prostego ze środkiem 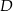D przeciwprostokątnej. Długość odcinka 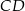CD jest równa
A) 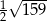1√ 1-59 2 B) 6,5 C) 13 D)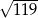 √ ---- 119

Rozwiązanie

Rozwiązanie tego zadania jest dostępne tylko dla użytkowników z wykupionym abonamentem.
Zaloguj się Informacje o abonamencie
Nie chcesz się rejestrować ani opłacać abonamentu? Zapłać przelewem 7,90 zł lub telefonicznie 9,90 zł, a otrzymasz dwudziestominutowy dostęp do wszystkich materiałów dostępnych w portalu.