/Szkoła średnia/Zadania testowe/Geometria/Planimetria/Trójkąt/Prostokątny/Oblicz długość

Zadanie nr 8589685

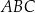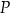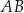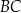Dwusieczne kątów ostrych trójkąta prostokątnego ABC przecinają się w punkcie P . Przyprostokątne AB i BC mają długości równe odpowiednio 12 i 9 (zobacz rysunek).

PIC

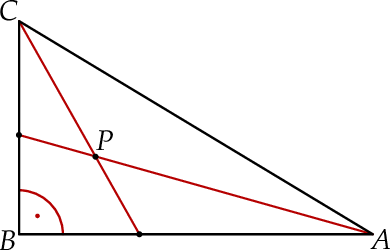
Odległość punktu 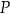P od przeciwprostokątnej 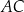AC jest równa
A) 3 B) 2 C) 15 D) 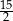15 2

Wersja PDF

Rozwiązanie

Punkt 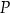P przecięcia się dwusiecznych trójkąta to środek okręgu wpisanego w ten trójkąt. W takim razie odległość punktu 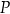P od boku 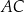AC jest równa promieniowi r tego okręgu. Zauważmy jeszcze, że

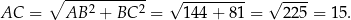
∘ ------------ √ --------- √ ---- AC = AB 2 + BC 2 = 144 + 81 = 225 = 15 .

Sposób I

Ze wzoru na pole 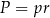P = pr , gdzie 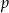p – połowa obwodu i r – promień okręgu wpisanego, obliczamy r .

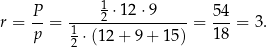
P 1 ⋅12 ⋅9 54 r = --= 1---2------------= ---= 3. p 2 ⋅(12 + 9 + 15) 18

Sposób II

Korzystamy ze wzoru na promień r okręgu wpisanego w trójkąt prostokątny:

r = a+--b−--c= 12-+-9-−-15-= 3. 2 2

 
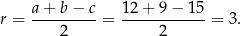
Odpowiedź: A

Wersja PDF