Zadanie nr 1462387
Największą liczbą całkowitą spełniającą nierówność 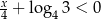 jest
jest
A) 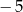 B)
B) 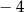 C)
C) 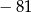 D)
D) 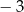
Rozwiązanie
Przekształćmy daną nierówność.
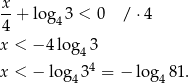
Zauważmy teraz, że 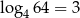 i
i 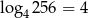 , więc
, więc 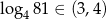 . Zatem największa liczba całkowita spełniająca powyższą nierówność to
. Zatem największa liczba całkowita spełniająca powyższą nierówność to 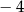
Odpowiedź: B

