/Szkoła średnia/Zadania testowe/Nierówności/Liniowe

Zadanie nr 8078046

Dodaj do ulubionych
Dodaj do rozwiązanych

Wskaż nierówność, której nie spełnia żadna liczba dodatnia.
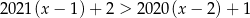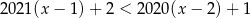
A) 202 1(x− 1)+ 2 > 2020 (x− 2)+ 1 B) 20 21(x − 1)+ 2 < 202 0(x− 2)+ 1
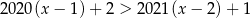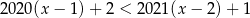
C) 2020 (x− 1)+ 2 > 2021(x − 2 )+ 1 D) 20 20(x − 1)+ 2 < 202 1(x− 2)+ 1

Rozwiązanie

Nierówności

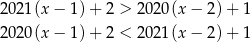
2021(x − 1) + 2 > 2020(x − 2) + 1 2020(x − 1) + 2 < 2021(x − 2) + 1

mogą być przekształcone do postaci 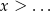x > ... , więc na pewno są spełnione przez nieskończenie wiele liczb dodatnich. Sprawdźmy dwie pozostałe nierówności

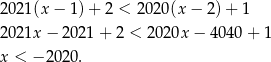
20 21(x− 1)+ 2 < 202 0(x− 2)+ 1 20 21x − 2021 + 2 < 2020x − 404 0+ 1 x < − 2020.

Tej nierówności nie spełnia więc żadna liczba dodatnia. Nie musimy tego robić, ale sprawdźmy jeszcze ostatnią z nierówności.

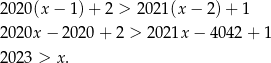
20 20(x− 1)+ 2 > 202 1(x− 2)+ 1 20 20x − 2020 + 2 > 2021x − 404 2+ 1 20 23 > x.

Ta nierówność ma oczywiście rozwiązania dodatnie.  
Odpowiedź: B

Wersja PDF