/Szkoła średnia/Zadania testowe/Geometria/Geometria analityczna/Różne

Zadanie nr 4218875

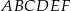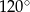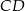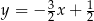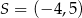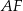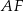Każdy kąt wewnętrzny sześciokąta ABCDEF ma miarę ∘ 120 . Bok CD tego sześciokąta jest zwarty w prostej o równaniu y = − 32x + 12 , a punkt S = (− 4,5) jest środkiem boku AF . Bok AF jest zawarty w prostej o równaniu
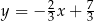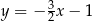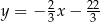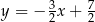
A) 2 7 y = − 3x+ 3 B) 3 y = − 2x− 1 C) 2 22 y = − 3x− 3- D) 3 7 y = − 2x + 2

Wersja PDF

Rozwiązanie

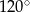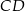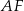Jeżeli naszkicujemy sześciokąt, w którym każdy kąt wewnętrzny ma miarę 12 0∘ (czyli tyle ile w sześciokącie foremnym), to robi się jasne, że boki CD i AF są równoległe.

PIC

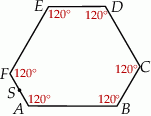
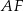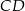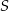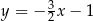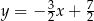W takim razie prosta AF jest równoległa do CD i przechodzi przez punkt S . To pozostawia nas z odpowiedziami: y = − 32x − 1 i y = − 32 x+ 72 . Łatwo sprawdzić, że pierwsza z tych prostych przechodzi przez punkt S .  
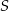Odpowiedź: B

Wersja PDF