/Szkoła średnia/Zadania testowe/Geometria/Geometria analityczna/Różne

Zadanie nr 9554031

Punkt 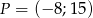P = (−8 ;15) znajduje się na końcowym ramieniu kąta α . Wówczas
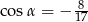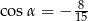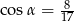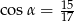
A) cosα = − 817 B) c osα = − 815 C) co sα = 8- 17 D) co sα = 15 17

Wersja PDF

Rozwiązanie

Szkicujemy opisaną sytuację.

PIC

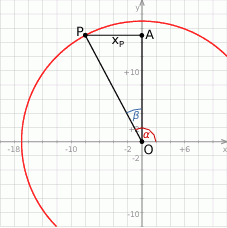
Sposób I

Korzystamy z definicji cosinusa.

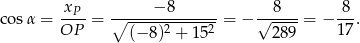
co sα = xP--= ∘----−-8-------= − √--8-- = − -8-. OP (− 8)2 + 152 2 89 1 7

Sposób II

Jeżeli 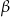β jest kątem jaki promień 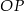OP tworzy z osią 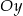Oy to mamy

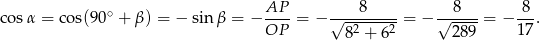
AP 8 8 8 cos α = cos(9 0∘ + β ) = − sin β = −----= − √---------= − √-----= − --. OP 82 + 62 289 17

 
Odpowiedź: A

Wersja PDF