/Szkoła średnia/Zadania testowe/Geometria/Geometria analityczna/Różne

Zadanie nr 9934177

Dodaj do ulubionych
Dodaj do rozwiązanych

Nierówność 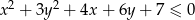2 2 x + 3y + 4x+ 6y + 7 ≤ 0 przedstawia na płaszczyźnie
A) punkt B) koło C) okrąg D) zbiór pusty

Rozwiązanie

Przekształcamy

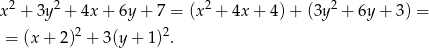
2 2 2 2 x + 3y + 4x + 6y + 7 = (x + 4x + 4)+ (3y + 6y+ 3) = = (x+ 2)2 + 3(y+ 1)2.

Zatem nierówność z zadania możemy zapisać w postaci

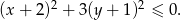
2 2 (x + 2) + 3 (y+ 1) ≤ 0.

Ponieważ lewa strona tej nierówności jest większa bądź równa 0, więc jedynym rozwiązaniem jest rozwiązanie równania

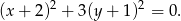
(x + 2)2 + 3 (y + 1 )2 = 0.

Stąd rozwiązaniem jest punkt 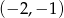(− 2,− 1) .  
Odpowiedź: A

Wersja PDF