Zadanie nr 5467677
Wierzchołki trójkąta 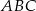 leżą na okręgu o środku
leżą na okręgu o środku 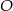 .
. 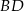 jest średnicą tego okręgu. Jeśli kąt
jest średnicą tego okręgu. Jeśli kąt 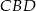 ma miarę
ma miarę 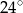 , to kąt
, to kąt 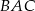 ma miarę
ma miarę
A) 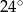 B)
B) 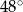 C)
C) 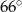 D)
D) 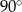
Rozwiązanie
Zaczynamy od rysunku
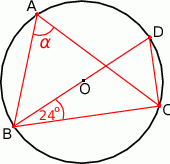
Ponieważ kąt 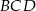 jest oparty na średnicy, więc
jest oparty na średnicy, więc
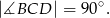
Teraz łatwo obliczyć miarę kąta 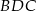
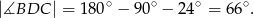
Teraz wystarczy zauważyć, że kąty 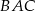 i
i 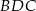 są kątami wpisanymi opartymi na tym samym łuku, więc są sobie równe
są kątami wpisanymi opartymi na tym samym łuku, więc są sobie równe
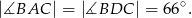
Odpowiedź: C

