Zadanie nr 5473257
Punkty 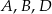 leżą na jednej prostej. Odcinek
leżą na jednej prostej. Odcinek 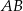 jest podstawą trójkąta równoramiennego
jest podstawą trójkąta równoramiennego  (zobacz rysunek).
(zobacz rysunek).
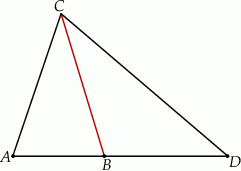
Jeżeli 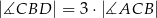 , to
, to 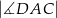 wynosi
wynosi
A) 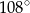 B)
B) 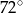 C)
C) 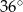 D)
D) 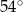
Rozwiązanie
Oznaczmy 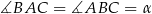 .
.
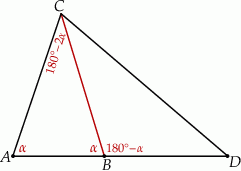
Mam wtedy
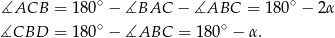
Wiemy ponadto, że
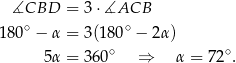
Odpowiedź: B
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Punkty 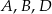 leżą na jednej prostej. Odcinek
leżą na jednej prostej. Odcinek 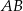 jest podstawą trójkąta równoramiennego
jest podstawą trójkąta równoramiennego  (zobacz rysunek).
(zobacz rysunek).

Jeżeli 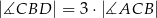 , to
, to 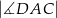 wynosi
wynosi
A) 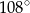 B)
B) 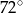 C)
C) 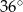 D)
D) 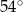
Oznaczmy 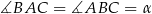 .
.

Mam wtedy
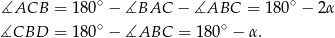
Wiemy ponadto, że
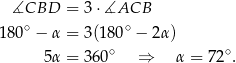
Odpowiedź: B
