/Szkoła średnia/Zadania testowe/Równania/Z wartością bezwzględną

Zadanie nr 3326388

Zbiór liczb, które na osi liczbowej są równoodległe od liczb 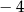− 4 i 10, można opisać za pomocą równania
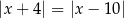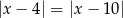
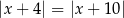A) |x + 4| = |x− 10| B) |x− 4| = |x − 1 0|
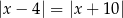
C) |x+ 4| = |x + 10| D) |x− 4| = |x+ 10|

Wersja PDF

Rozwiązanie

Sposób I

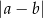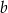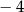Przypomnijmy, że liczba |a − b| oznacza odległość między liczbami a i b . Zatem odległości liczby x od liczb − 4 i 10 możemy zapisać w postaci

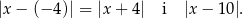
|x− (− 4)| = |x + 4 | i |x − 10 |.

Zatem szukanym równaniem jest

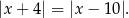
|x+ 4| = |x − 1 0|.

Sposób II

Liczbą, która jest równoodległa od liczb 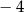− 4 i 10 jest dokładnie środek przedziału 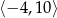⟨− 4,10 ⟩ , czyli liczba

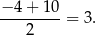
−-4-+-10- 2 = 3.

Teraz wystarczy sprawdzić, którą z podanych równości spełnia 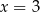x = 3 .  
Odpowiedź: A

Wersja PDF