/Szkoła średnia/Zadania testowe/Zadania z treścią/Różne

Zadanie nr 4857245

W grupie 90 osób 60 włada językiem angielskim, 40 – językiem niemieckim, 32 – językiem francuskim, 21 – angielskim i niemieckim, 19 – angielskim i francuskim, 12 – niemieckim i francuskim. Ile osób włada wszystkimi trzema wymienionymi językami?
A) 4 B) 8 C) 6 D) 10

Wersja PDF

Rozwiązanie

Sposób I

Zaczynamy od rysunku pomocniczego

PIC

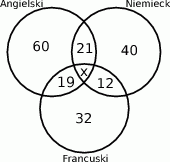
Obliczamy liczbę osób władających wyłącznie angielskim

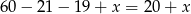
60 − 21 − 19 + x = 20+ x

(w grupie jest 60 znających angielski od tej liczby odejmujemy osoby znające angielski i niemiecki oraz znające angielski i francuski. Musimy dodać osoby znające wszystkie trzy języki ponieważ w grupie znającej angielski i niemiecki znajdują się osoby znające trzy języki podobnie jest z grupą znającą angielski i francuski, czyli dwukrotnie odjeliśmy grupę władającą trzema językami).
Obliczamy liczbę osób władających wyłącznie niemieckim

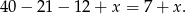
40 − 21 − 1 2+ x = 7 + x.

Obliczamy liczbę osób władających wyłącznie francuskim

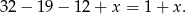
32 − 19 − 1 2+ x = 1 + x.

Obliczamy ile osób włada dokładnie dwoma językami

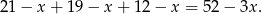
21 − x + 19 − x + 12 − x = 52 − 3x.

Łącznie osób znających wyłącznie jeden język, osób znających dokładnie dwa języki i osób znających wszystkie trzy jest 90. Zatem

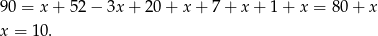
90 = x+ 52− 3x + 20 + x + 7 + x + 1 + x = 8 0+ x x = 10.

Sposób II

Korzystamy ze wzoru

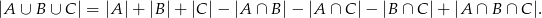
|A ∪ B ∪ C | = |A |+ |B |+ |C |− |A ∩ B |− |A ∩ C |− |B ∩ C |+ |A ∩ B ∩ C |.

W naszej sytuacji mamy

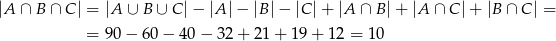
|A ∩ B ∩ C | = |A ∪ B ∪ C|− |A |− |B |− |C |+ |A ∩ B |+ |A ∩ C |+ |B ∩ C | = = 9 0− 6 0− 40− 32+ 21+ 19 + 12 = 1 0

 
Odpowiedź: D

Wersja PDF