Zadanie nr 3057212
W ilu ćwiartkach układu współrzędnych znajdują się punkty okręgu o równaniu
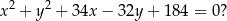
A) W jednej. B) W dwóch. C) W trzech. D) W czterech.
Rozwiązanie
Zapiszmy równanie okręgu tak, aby było widać jaki jest środek i promień.
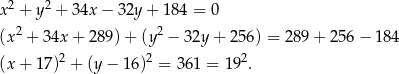
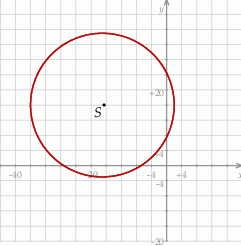
Jest to więc okrąg o środku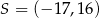 
i promieniu 
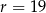. Środek tego okręgu jest zawarty w II ćwiartce, więc oczywiście w tej ćwiartce znajdują się punkty tego okręgu. Ponadto, odległość punktu 
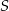od obu osi jest mniejsza od promienia, więc okrąg ten przechodzi też przez sąsiednie ćwiartki: I i III. Ponieważ jednak
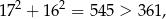
okrąg ten nie przechodzi przez IV ćwiartkę.
Odpowiedź: C
