/Szkoła średnia/Zadania testowe/Geometria/Geometria analityczna/Okrąg

Zadanie nr 4226694

Dodaj do ulubionych
Dodaj do rozwiązanych

Liczba punktów wspólnych okręgu o równaniu 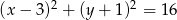2 2 (x− 3) + (y+ 1) = 16 z osiami układu współrzędnych jest równa
A) 0 B) 1 C) 2 D) 4

Rozwiązanie

Sposób I

Nie jest trudno naszkicować dany okrąg: jest to okrąg o środku 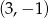(3,− 1) i promieniu 4.

PIC

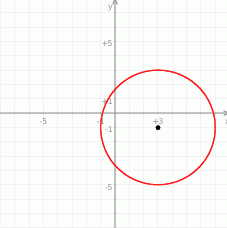
Gdy to zrobimy to widać, że przecina on każdą z osi w dwóch punktach.

Sposób II

Punkty wspólne danego okręgu z osią 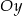Oy otrzymamy wstawiając do jego równania x = 0 .

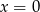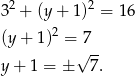
2 2 3 + (y+ 1) = 16 (y+ 1)2 = 7 √ -- y+ 1 = ± 7.

Widać, że są dwa punkty przecięcia.

Podobnie, aby wyznaczyć punkty wspólne z osią 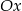Ox wystarczy podstawić w równaniu okręgu y = 0 .

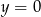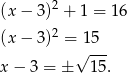
(x − 3)2 + 1 = 1 6 2 (x − 3) = 1 5 √ --- x − 3 = ± 15.

Widać, że są dwa kolejne punkty przecięcia.  
Odpowiedź: D

Wersja PDF