Zadanie nr 5991873
Okrąg o równaniu 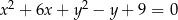 przesunięto o wektor
przesunięto o wektor ![[ 13] 9,− 2](https://img.zadania.info/zad/5991873/HzadT1x.gif) . Środek otrzymanego w ten sposób okręgu ma współrzędne
. Środek otrzymanego w ten sposób okręgu ma współrzędne
A) 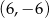 B)
B) 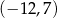 C)
C) 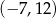 D)
D) 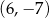
Rozwiązanie
Przekształćmy dane równanie okręgu tak, aby było widać jaki jest jego środek i promień
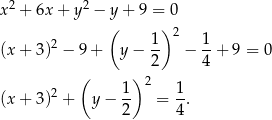
Jest to więc okrąg o środku 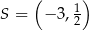 i promieniu
i promieniu 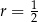 . Szkicujemy tę sytuację.
. Szkicujemy tę sytuację.
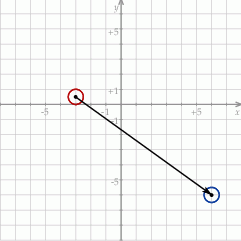
Jeżeli 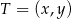 jest środkiem przesuniętego okręgu, to mamy
jest środkiem przesuniętego okręgu, to mamy
![[ ] −→ [ ] 9,− 13- = ST = x + 3,y − 1- . 2 2](https://img.zadania.info/zad/5991873/HzadR5x.gif)
Stąd
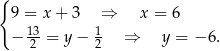
Zatem 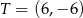 .
.
Odpowiedź: A

