/Szkoła średnia/Zadania testowe/Geometria/Geometria analityczna/Okrąg

Zadanie nr 6287620

Dodaj do ulubionych
Dodaj do rozwiązanych

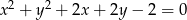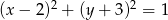
Okręgi 2 2 x + y + 2x + 2y − 2 = 0 oraz 2 2 (x − 2) + (y + 3) = 1
A) są styczne zewnętrznie B) są styczne wewnętrznie C) są rozłączne D) przecinają się

Rozwiązanie

Drugi okrąg to okrąg o środku 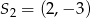S 2 = (2,− 3) i promieniu 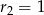r2 = 1 . Przekształćmy równanie pierwszego okręgu, żeby zobaczyć jaki ma środek i promień.

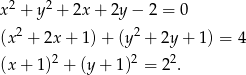
x2 + y2 + 2x + 2y − 2 = 0 2 2 (x + 2x + 1) + (y + 2y + 1) = 4 (x + 1)2 + (y + 1)2 = 22.

Jest to więc okrąg o środku 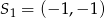S = (− 1,− 1) 1 i promieniu r = 2 1 .

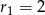Sposób I

Szkicujemy okręgi, aby ustalić jakie jest ich wzajemne położenie.

PIC

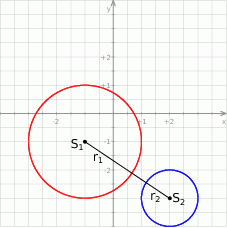
Sposób II

Obliczmy odległość między środkami okręgów.

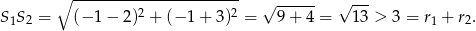
∘ ----------------------- --- S S = (− 1 − 2)2 + (− 1 + 3)2 = √ 9-+-4-= √ 13 > 3 = r + r . 1 2 1 2

Ponieważ odległość między środkami okręgów jest większa niż suma ich promieni, okręgi są rozłączne.  
Odpowiedź: C

Wersja PDF