/Szkoła średnia/Zadania testowe/Geometria/Geometria analityczna/Okrąg

Zadanie nr 9830066

Dodaj do ulubionych
Dodaj do rozwiązanych

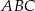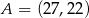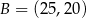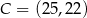
Wskaż równanie okręgu opisanego na trójkącie ABC o wierzchołkach A 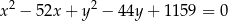= (27 ,2 2) , B = (25,20) , C = (25 ,2 2)
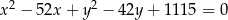
A) x2 − 52x + y2 − 4 4y+ 1159 = 0 B) x 2 − 52x + y2 − 42y+ 1115 = 0
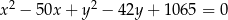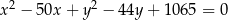
C) 2 2 x − 50x + y − 42y + 1065 = 0 D) 2 2 x − 50x + y − 44y+ 1065 = 0

Rozwiązanie

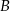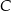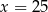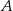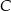Zauważmy, że pierwsze współrzędne punktów B i C są równe, więc punkty te leżą na pionowej prostej x = 25 . Podobnie stwierdzamy, że punkty A i C leżą na poziomej prostej 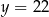y = 22 . To oznacza, że trójkąt 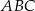ABC jest prostokątny i 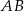AB jest jego przeciwprostokątną.

PIC

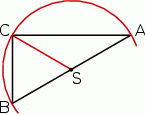
Środkiem okręgu opisanego na trójkącie prostokątnym jest środek jego przeciwprostokątnej, czyli punkt

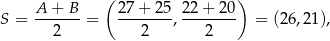
( ) S = A-+--B-= 2-7+-2-5, 22-+-20 = (26,21), 2 2 2

a promień tego okręgu to połowa długości przeciwprostokątnej

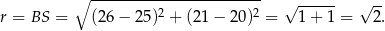
∘ ------------------------ r = BS = (26 − 25)2 + (21 − 20)2 = √ 1-+-1-= √ 2.

Interesujący nas okrąg ma więc równanie

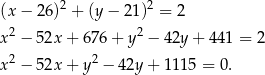
2 2 (x− 26) + (y− 21) = 2 x2 − 52x + 676 + y2 − 42y + 4 41 = 2 x2 − 52x + y2 − 42y + 11 15 = 0.

 
Odpowiedź: B

Wersja PDF