/Szkoła średnia/Zadania testowe/Geometria/Geometria analityczna/Okrąg

Zadanie nr 9973924

Dodaj do ulubionych
Dodaj do rozwiązanych

Okrąg o środku 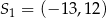S1 = (− 13 ,1 2) oraz okrąg o środku 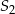S2 i promieniu 8 są styczne zewnętrznie w punkcie 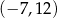(−7 ,12) . Wtedy
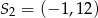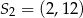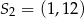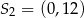
A) S 2 = (− 1,12) B) S 2 = (2,12) C) S = (1,1 2) 2 D) S = (0,12) 2

Rozwiązanie

Szkicujemy opisaną sytuację.

PIC

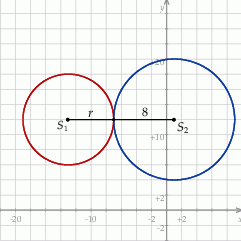
Zauważmy, że środek 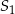S1 i punkt styczności leżą na tej samej poziomej prostej 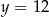y = 12 . W takim razie punkt 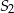S2 też leży na tej prostej, więc jego druga współrzędna jet równa 12. Ponadto, odległość 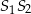S S 1 2 między środkami okręgów stycznych zewnętrznie jest równa sumie ich promieni, czyli jest równa

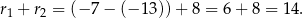
r1 + r2 = (− 7− (−1 3))+ 8 = 6+ 8 = 14.

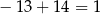To oznacza, że pierwsza współrzędna punktu S2 musi być równa − 13 + 14 = 1 .  
Odpowiedź: C

Wersja PDF