/Szkoła średnia/Zadania testowe/Ciągi

Zadanie nr 1312673

Dodaj do ulubionych
Dodaj do rozwiązanych

Dany jest ciąg geometryczny 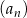(an) o wszystkich wyrazach niezerowych i pierwszym wyrazie 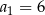a1 = 6 . Jeżeli 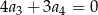4a3 + 3a4 = 0 , to wzorem ogólnym ciągu 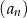(an) jest
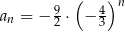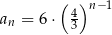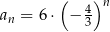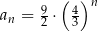
A) 9 ( 4)n an = − 2 ⋅ − 3 B) (4)n −1 an = 6 ⋅ 3 C) ( 4)n an = 6 ⋅ − 3 D) 9 (4)n an = 2 ⋅ 3

Rozwiązanie

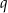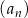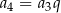Jeżeli oznaczymy przez q iloraz ciągu (an) , to a4 = a3q i z podanego warunku mamy

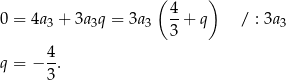
( ) 0 = 4a 3 + 3a 3q = 3a3 4+ q / : 3a3 3 4 q = − -. 3

Wyraz ogólny ciągu jest więc równy

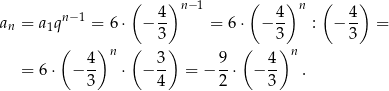
( 4)n −1 ( 4 )n ( 4 ) an = a1qn−1 = 6 ⋅ − -- = 6⋅ − -- : − -- = ( ) ( 3) ( 3) 3 4 n 3 9 4 n = 6⋅ − -- ⋅ − -- = − --⋅ − -- . 3 4 2 3

 
Odpowiedź: A

Wersja PDF