/Szkoła średnia/Zadania testowe/Ciągi

Zadanie nr 3448427

Dodaj do ulubionych
Dodaj do rozwiązanych

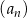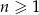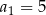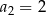W ciągu arytmetycznym (an) , określonym dla każdej liczby naturalnej n ≥ 1 , są dane dwa wyrazy: a1 = 5 i a 2 = 2 . Stąd wynika, że n –ty wyraz tego ciągu jest określony wzorem
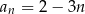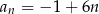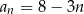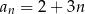
A) an = 2− 3n B) an = − 1+ 6n C) an = 8 − 3n D) an = 2 + 3n

Rozwiązanie

Sposób I

Przypomnijmy, że wzór na ogólny wyraz ciągu arytmetycznego, to

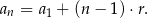
an = a1 + (n − 1) ⋅r.

Wyznaczamy różnicę r ciągu (an) .

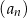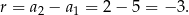
r = a2 − a1 = 2 − 5 = − 3.

Teraz już łatwo zapisać wzór na ogólny wyraz tego ciągu.

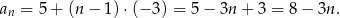
an = 5+ (n − 1) ⋅(− 3) = 5− 3n + 3 = 8 − 3n .

Sposób II

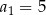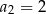Sprawdzamy, który wzór daje a1 = 5 i a2 = 2 . Tak jest tylko w przypadku wzoru

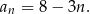
an = 8 − 3n .

 
Odpowiedź: C

Wersja PDF