/Szkoła średnia/Zadania testowe/Ciągi

Zadanie nr 4420003

Dodaj do ulubionych
Dodaj do rozwiązanych

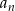Ciąg an dany jest wzorem 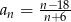n−18- an = n+ 6 , gdzie 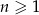n ≥ 1 . Liczba wyrazów całkowitych tego ciągu to
A) 2 B) 3 C) 4 D) 6

Rozwiązanie

Jeżeli zapiszemy wyraz ciągu w postaci

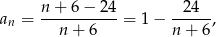
n + 6− 24 24 an = -----------= 1− -----, n + 6 n+ 6

to widać, że 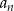an będzie liczbą całkowitą tylko wtedy, gdy 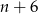n + 6 dzieli 24, czyli 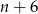n + 6 musi być jedną z liczb: 8, 12, 24 . Tak będzie gdy

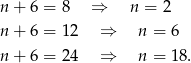
n + 6 = 8 ⇒ n = 2 n + 6 = 12 ⇒ n = 6 n + 6 = 24 ⇒ n = 18 .

Zatem trzy wyrazy ciągu są liczbami całkowitymi.  
Odpowiedź: B

Wersja PDF