Zadanie nr 4784079
W ciągu geometrycznym 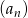 , określonym dla
, określonym dla 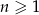 , dane są:
, dane są: 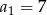 ,
, 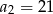 . Wtedy
. Wtedy
A) 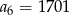 B)
B) 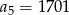 C)
C) 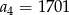 D)
D) 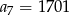
Rozwiązanie
Iloraz ciągu 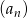 jest równy
jest równy
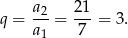
Stąd
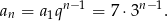
Sposób I
Sprawdzamy, który wyraz ciągu jest równy 1701.
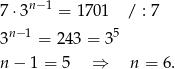
Sposób II
Ze wzoru na  –ty wyraz ciągu
–ty wyraz ciągu 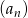 mamy
mamy
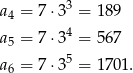
Odpowiedź: A

