/Szkoła średnia/Zadania testowe/Ciągi

Zadanie nr 5524892

Dodaj do ulubionych
Dodaj do rozwiązanych

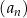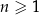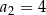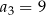Ciąg arytmetyczny (an) jest określony dla każdej liczby naturalnej n ≥ 1 . W tym ciągu a2 = 4 oraz a3 = 9 . Szósty wyraz ciągu 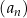(an) jest równy
A) 24 B) 29 C) 36 D) 69

Rozwiązanie

Sposób I

Jeżeli r jest różnicą danego ciągu arytmetycznego, to

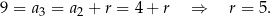
9 = a3 = a2 + r = 4+ r ⇒ r = 5.

W takim razie

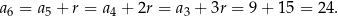
a6 = a5 + r = a4 + 2r = a3 + 3r = 9 + 15 = 2 4.

Sposób II

Ze wzoru 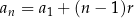an = a1 + (n − 1)r na n -ty wyraz ciągu arytmetycznego mamy

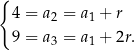
{ 4 = a 2 = a1 + r 9 = a 3 = a1 + 2r.

Odejmujemy od drugiego równania pierwsze i mamy

5 = r.

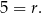
Z pierwszego równania: 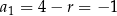a1 = 4 − r = − 1 . Zatem

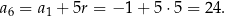
a 6 = a1 + 5r = − 1+ 5⋅5 = 24.

 
Odpowiedź: A

Wersja PDF