/Szkoła średnia/Zadania testowe/Ciągi

Zadanie nr 5944480

Dodaj do ulubionych
Dodaj do rozwiązanych

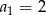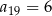W ciągu arytmetycznym a1 = 2 oraz a19 = 6 . Wtedy suma 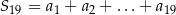S 19 = a1 + a2 + ...+ a19 jest równa
A) 76 B) 80 C) 152 D) 160

Rozwiązanie

Sposób I

Korzystamy ze wzoru

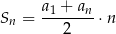
a1 + an Sn = -------⋅ n 2

na sumę n początkowych wyrazów ciągu arytmetycznego. Mamy zatem

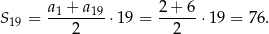
a1 + a19 2 + 6 S 19 = --------⋅ 19 = ------⋅19 = 76. 2 2

Sposób II

Ze wzoru 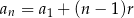an = a1 + (n − 1)r na n -ty wyraz ciągu arytmetycznego mamy

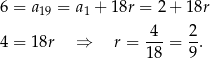
6 = a19 = a1 + 18r = 2 + 18r 4 2 4 = 18r ⇒ r = ---= -. 18 9

Korzystamy teraz ze wzoru na sumę n początkowych wyrazów ciągu arytmetycznego.

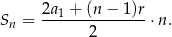
2a + (n − 1)r Sn = --1------------⋅n. 2

Mamy zatem

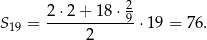
2 ⋅2 + 18 ⋅ 2 S19 = -----------9 ⋅19 = 7 6. 2

 
Odpowiedź: A

Wersja PDF