Zadanie nr 6335287
Wzorem ogólnym ciągu geometrycznego w którym 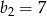 i
i 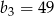 jest:
jest:
A) 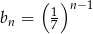 B)
B) 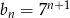 C)
C) 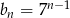 D)
D) 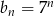
Rozwiązanie
Sposób I
Ponieważ mamy podane dwa kolejny wyrazy ciągu geometrycznego, łatwo jest obliczyć jego iloraz
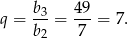
Z podanego drugiego wyrazu obliczamy 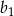 .
.
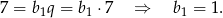
Zatem
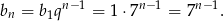
Sposób II
W każdym z podanych wzorów podstawiamy 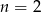 i sprawdzamy, czy wychodzi 7. Wyjdzie tylko we wzorze z podpunktu C.
i sprawdzamy, czy wychodzi 7. Wyjdzie tylko we wzorze z podpunktu C.
Odpowiedź: C

