/Szkoła średnia/Zadania testowe/Ciągi

Zadanie nr 7692894

Dodaj do ulubionych
Dodaj do rozwiązanych

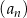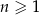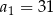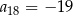W ciągu arytmetycznym (an) , określonym dla n ≥ 1 , dane są dwa wyrazy: a1 = 3 1 oraz a 18 = −1 9 . Suma osiemnastu początkowych wyrazów tego ciągu jest równa
A) 102 B) 108 C) 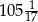105 1- 17 D) − 171

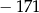
Rozwiązanie

Sposób I

Korzystamy ze wzoru

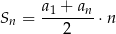
a1 + an Sn = -------⋅ n 2

na sumę n początkowych wyrazów ciągu arytmetycznego. Mamy zatem

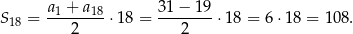
a1 + a18 3 1− 19 S18 = -------- ⋅18 = --------⋅ 18 = 6 ⋅18 = 10 8. 2 2

Sposób II

Ze wzoru 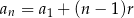an = a1 + (n − 1)r na n -ty wyraz ciągu arytmetycznego mamy

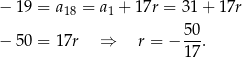
− 19 = a18 = a1 + 17r = 31+ 17r 50 − 50 = 17r ⇒ r = − --. 17

Korzystamy teraz ze wzoru na sumę n początkowych wyrazów ciągu arytmetycznego.

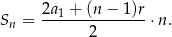
2a + (n − 1)r Sn = --1------------⋅n. 2

Mamy zatem

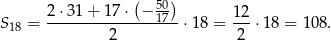
2⋅3 1+ 1 7⋅(− 50-) 12 S18 = ---------------17--⋅ 18 = ---⋅18 = 108. 2 2

 
Odpowiedź: B

Wersja PDF