/Szkoła średnia/Zadania testowe/Ciągi

Zadanie nr 7784388

Dodaj do ulubionych
Dodaj do rozwiązanych

Suma n początkowych liczb naturalnych dodatnich podzielnych przez 3 jest równa
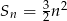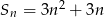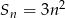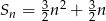
A) Sn = 32n2 B) Sn = 3n2 + 3n C) S = 3n2 n D) S = 3n 2 + 3n n 2 2

Rozwiązanie

Liczby naturalne podzielne przez 3 tworzą ciąg arytmetyczny o pierwszym wyrazie 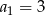a1 = 3 i różnicy 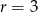r = 3 . Liczymy sumę n początkowych wyrazów tego ciągu.

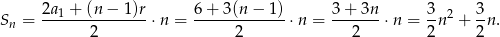
2a1 +-(n−--1)r- 6-+-3(n-−--1) 3-+-3n- 3- 2 3- Sn = 2 ⋅ n = 2 ⋅n = 2 ⋅n = 2 n + 2n .

 
Odpowiedź: D

Wersja PDF