Zadanie nr 9605657
W malejącym ciągu geometrycznym 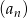 mamy
mamy 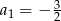 i
i 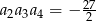 . Iloraz tego ciągu równy
. Iloraz tego ciągu równy
A) 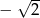 B)
B) 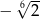 C)
C) 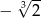 D)
D) 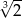
Rozwiązanie
Ponieważ 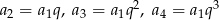 mamy równanie
mamy równanie
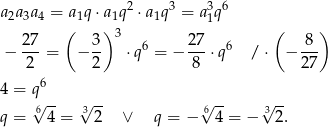
Ponieważ ciąg ma być malejący mamy 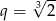 (bo
(bo 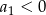 ).
).
Odpowiedź: D
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
W malejącym ciągu geometrycznym 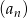 mamy
mamy 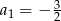 i
i 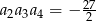 . Iloraz tego ciągu równy
. Iloraz tego ciągu równy
A) 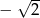 B)
B) 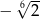 C)
C) 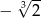 D)
D) 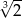
Ponieważ 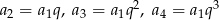 mamy równanie
mamy równanie
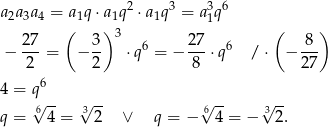
Ponieważ ciąg ma być malejący mamy 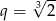 (bo
(bo 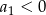 ).
).
Odpowiedź: D
