Zadanie nr 9630160
Ciąg 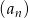 określony jest wzorem
określony jest wzorem 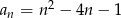 , gdzie
, gdzie 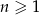 . Liczba ujemnych wyrazów tego ciągu jest równa
. Liczba ujemnych wyrazów tego ciągu jest równa
A) 2 B) 3 C) 4 D) 5
Rozwiązanie
Rozwiązujemy nierówność
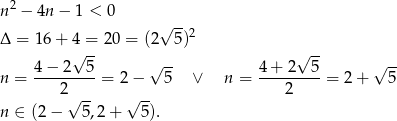
Ponieważ 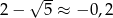 i
i 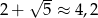 wyrazami ujemnymi są:
wyrazami ujemnymi są: 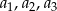 i
i 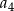 .
.
Odpowiedź: C
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Ciąg 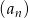 określony jest wzorem
określony jest wzorem 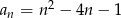 , gdzie
, gdzie 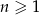 . Liczba ujemnych wyrazów tego ciągu jest równa
. Liczba ujemnych wyrazów tego ciągu jest równa
A) 2 B) 3 C) 4 D) 5
Rozwiązujemy nierówność
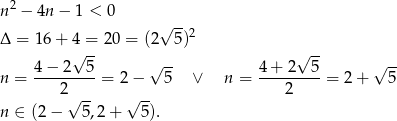
Ponieważ 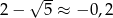 i
i 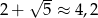 wyrazami ujemnymi są:
wyrazami ujemnymi są: 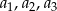 i
i 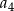 .
.
Odpowiedź: C
