/Szkoła średnia/Zadania testowe/Ciągi

Zadanie nr 9683631

Dodaj do ulubionych
Dodaj do rozwiązanych

Dany jest nieskończony ciąg 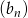(bn) , dla którego 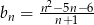n2−5n−-6 bn = n+ 1 . Wobec tego wszystkie wyrazy tego ciągu są liczbami
A) dodatnimi B) ujemnymi C) całkowitymi D) niewymiernymi

Rozwiązanie

Wyznaczamy pierwiastki licznika

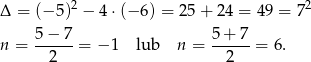
2 2 Δ = (− 5) − 4 ⋅(− 6) = 25 + 24 = 49 = 7 5-−-7- 5+--7- n = 2 = − 1 lub n = 2 = 6.

Zatem wzór na ciąg 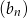(bn) możemy zapisać w postaci

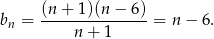
(n-+-1)(n-−-6)- bn = n + 1 = n − 6.

Teraz widać, że wyrazy ciągu 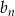bn są liczbami całkowitymi.  
Odpowiedź: C

Wersja PDF