/Szkoła średnia/Nierówności/Wielomianowe

Zadanie nr 3835630

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż nierówność

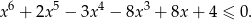
6 5 4 3 x + 2x − 3x − 8x + 8x + 4 ≤ 0.

Rozwiązanie

Musimy rozłożyć wielomian z lewej strony nierówności. Aby to zrobić szukamy jego pierwiastków wymiernych – sprawdzamy dzielniki wyrazu wolnego. Łatwo zauważyć, że jednym z pierwiastków jest 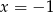x = − 1 . Dzielimy więc wielomian przez 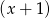(x + 1) – my zrobimy to grupując wyrazy

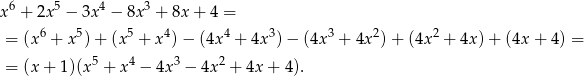
x6 + 2x5 − 3x4 − 8x 3 + 8x + 4 = = (x6 + x5) + (x5 + x4) − (4x4 + 4x 3) − (4x 3 + 4x 2)+ (4x 2 + 4x)+ (4x + 4) = 5 4 3 2 = (x + 1)(x + x − 4x − 4x + 4x + 4).

Gołym okiem widać teraz, że wielomian w drugim nawiasie dzieli się przez 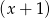(x + 1) , wykonujemy to dzielenie.

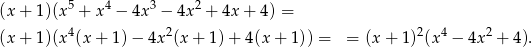
(x+ 1)(x5 + x4 − 4x3 − 4x2 + 4x + 4) = (x+ 1)(x4(x + 1)− 4x2(x + 1) + 4(x + 1)) = = (x + 1 )2(x4 − 4x2 + 4).

Teraz łatwo zauważyć, że wielomian w drugim z nawiasów to pełen kwadrat.

[ √ -- √ --]2 (x+ 1)2(x4− 4x 2+ 4) = (x+ 1 )2(x 2− 2)2 = (x + 1)2 (x − 2)(x + 2) .

Dana nierówność jest więc równoważna nierówności

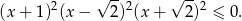
√ -- √ -- (x + 1 )2(x − 2)2(x+ 2)2 ≤ 0.

Jej rozwiązaniem jest więc zbiór 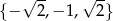√ -- √ -- {− 2,− 1, 2} .  
Odpowiedź: √ -- √ -- {− 2,− 1, 2 }

Wersja PDF