/Szkoła średnia/Nierówności/Wielomianowe

Zadanie nr 4768526

Dodaj do ulubionych
Dodaj do rozwiązanych

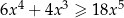Wyznacz wszystkie liczby dodatnie x spełniające nierówność 4 3 5 6x + 4x ≥ 1 8x .

Rozwiązanie

Ponieważ interesują nas tylko liczby dodatnie, możemy podzielić daną nierówność stronami przez 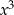x3 .

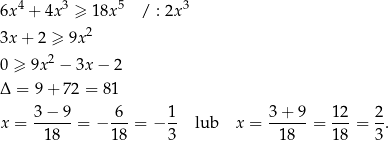
6x 4 + 4x 3 ≥ 18x5 / : 2x3 2 3x + 2 ≥ 9x 0 ≥ 9x 2 − 3x− 2 Δ = 9 + 72 = 81 3−--9- -6- 1- 3-+-9- 12- 2- x = 18 = − 1 8 = − 3 lub x = 18 = 18 = 3.

Ponieważ współczynnik przy 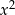x2 jest dodatni, wykres tego trójmianu jest parabolą o ramionach skierowanych do góry, jest on więc poniżej osi 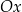Ox na przedziale [ ] − 13, 23 .

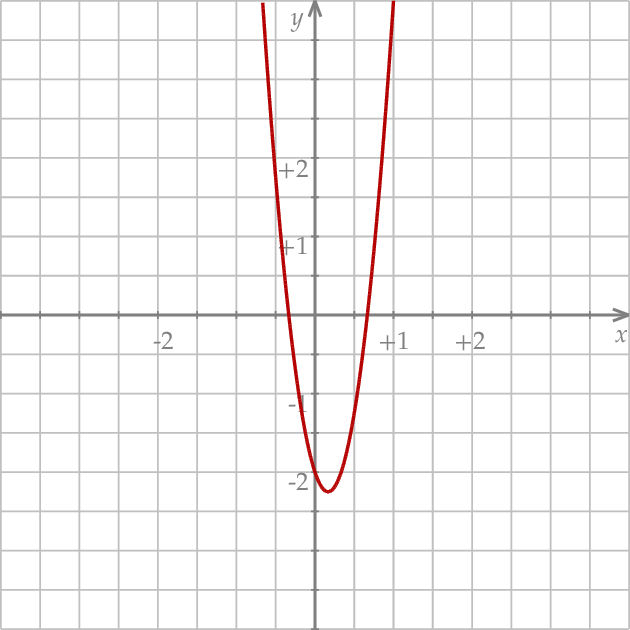
ZINFO-FIGURE

Z założenia interesują nas jednak tylko rozwiązania dodatnie, więc rozwiązaniem nierówności jest przedział ( ] 0, 23 .  
Odpowiedź: x ∈ (0 , 2] 3

Wersja PDF