/Szkoła średnia/Nierówności/Wielomianowe

Zadanie nr 6426510

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż nierówność 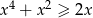4 2 x + x ≥ 2x .

Rozwiązanie

Przekształcamy daną nierówność.

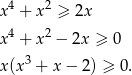
4 2 x + x ≥ 2x x4 + x2 − 2x ≥ 0 3 x(x + x − 2) ≥ 0 .

Widać, że wielomian w nawiasie zeruje się dla 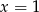x = 1 , więc dzielimy go przez dwumian 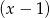(x − 1) . My zrobimy to grupując wyrazy.

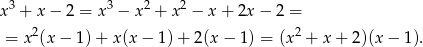
x3 + x − 2 = x 3 − x 2 + x 2 − x + 2x − 2 = 2 2 = x (x − 1 )+ x (x− 1)+ 2(x− 1) = (x + x + 2)(x − 1).

Zauważmy, że trójmian w pierwszym nawiasie jest zawsze dodatni, bo 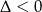Δ < 0 . Daną nierówność możemy więc zapisać w postaci

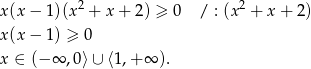
x(x − 1)(x2 + x + 2) ≥ 0 / : (x2 + x + 2) x(x − 1) ≥ 0 x ∈ (− ∞ ,0⟩∪ ⟨1,+ ∞ ).

 
Odpowiedź: x ∈ (− ∞ ,0⟩ ∪ ⟨1,+ ∞ )

Wersja PDF