/Szkoła średnia/Nierówności/Wielomianowe

Zadanie nr 6754277

Rozwiąż nierówność

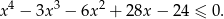
4 3 2 x − 3x − 6x + 28x − 24 ≤ 0.
Wersja PDF

Rozwiązanie

Szukamy pierwiastków lewej strony wśród dzielników wyrazu wolnego. Kilka prób i znajdujemy 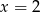x = 2 . Dzielimy więc wielomian z lewej strony przez 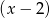(x − 2) . My zrobimy to grupując wyrazy.

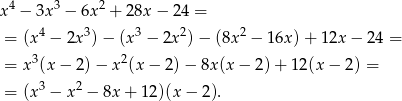
x 4 − 3x 3 − 6x2 + 28x − 24 = 4 3 3 2 2 = (x − 2x )− (x − 2x ) − (8x − 16x )+ 12x − 24 = = x3(x − 2)− x2(x − 2) − 8x(x − 2 )+ 12 (x− 2) = 3 2 = (x − x − 8x+ 12)(x − 2).

Ponownie szukamy pierwiastka wielomianu stopnia 3 w pierwszym nawiasie. Łatwo sprawdzić, że jednym z nich jest 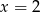x = 2 . Dzielimy dalej.

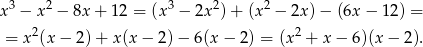
x3 − x2 − 8x + 12 = (x3 − 2x2)+ (x2 − 2x) − (6x − 12) = = x2(x − 2 )+ x (x− 2)− 6(x− 2) = (x2 + x − 6)(x − 2).

Pozostało teraz rozłożyć trójmian w pierwszym nawiasie.

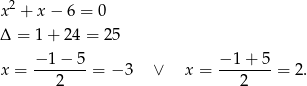
x2 + x − 6 = 0 Δ = 1+ 24 = 25 x = −-1−-5-= − 3 ∨ x = −-1+--5 = 2. 2 2

Zatem

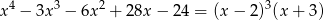
4 3 2 3 x − 3x − 6x + 28x − 2 4 = (x − 2) (x + 3)

i wyjściową nierówność możemy zapisać w postaci

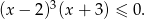
3 (x − 2) (x + 3) ≤ 0.

Jest ona równoważna nierówności

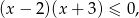
(x − 2 )(x+ 3) ≤ 0,

czyli jej rozwiązaniem jest przedział 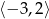⟨− 3,2⟩ .  
Odpowiedź: x ∈ ⟨− 3,2⟩

Wersja PDF