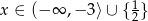/Szkoła średnia/Nierówności/Wielomianowe

Zadanie nr 7130601

Rozwiąż nierówność 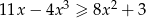3 2 11x − 4x ≥ 8x + 3 .

Wersja PDF

Rozwiązanie

Zapisujemy nierówność w postaci

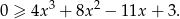
3 2 0 ≥ 4x + 8x − 11x + 3.

Aby rozłożyć prawą stronę szukamy najpierw jej pierwiastków całkowitych. Sprawdzając dzielniki wyrazu wolnego znajdujemy pierwiastek 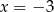x = − 3 . Dzielimy więc wielomian z prawej strony przez 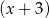(x + 3) . My zrobimy to grupując wyrazy.

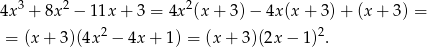
4x3 + 8x2 − 11x + 3 = 4x2(x + 3) − 4x(x + 3)+ (x + 3 ) = 2 2 = (x + 3)(4x − 4x + 1 ) = (x+ 3)(2x − 1) .

Mamy zatem nierówność

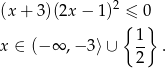
2 (x+ 3)(2x − 1) ≤ 0 { 1 } x ∈ (− ∞ ,− 3⟩∪ -- . 2

 
Odpowiedź: x ∈ (− ∞ ,− 3⟩ ∪ {12}

Wersja PDF